Треугольник квадрат: Круг, квадрат, треугольник… Кто он, мой ребенок? – Как найти площадь треугольника — Лайфхакер

Круг, квадрат, треугольник… Кто он, мой ребенок?

Перед вами — так называемый психогеометрический тест С.Деллингер (адаптация А.А. Алексеева, Л.А. Громовой). Тест направлен на оценку черт характера, модели поведения и стиля жизни человека с помощью простейших геометрических фигур. Но мы вам предлагаем воспользоваться им более широко.

Для этого сначала выполните тест от своего имени. Затем представьте, как, на ваш взгляд, его выполнил бы ваш ребенок. Запишите результат. И в заключение предложите выполнить тест ему самому. 

Ну как? Все совпало? Или его выбор стал для вас неожиданностью?

Не лишним будет также подумать об особенностях взаимодействия с подростком по итогам теста, о положительных моментах и о тех точках, в которых надо быть осторожнее и внимательнее. 

ИТАК, инструкция:

Посмотрите на пять фигур: квадрат, треугольник, прямоугольник, круг, зигзаг.

Выберите из них ту, которая первой привлекла Вас. Присвойте ей №1. Теперь рассортируйте оставшиеся четыре фигуры в порядке вашего предпочтения и запишите их названия под соответствующими номерами. Фигура, которую вы поместили на первое место, это Ваша

основная фигура, или субъективная форма. Она олицетворяет Ваши главные, доминирующие черты характера и особенности поведения. Остальные четыре фигуры – это своеобразные модуляторы, они могут окрашивать ведущую мелодию Вашего поведения. Сила их влияния убывает с увеличением порядкового номера.

Ни одна фигура Вам полностью не подходит? Тогда Вас можно описать комбинацией из двух или даже трех форм – такое не редкость. Обратите внимание также на последнюю фигуру — она указывает на форму человека, с которым вам будет труднее всего взаимодействовать

         

Квадрат – неутомимый труженик! Трудолюбие, усердие, позволяющее добиваться завершения работы, — вот чем, прежде всего, знамениты истинные Квадраты. Выносливость, терпение и методичность обычно делают Квадрата высококлассным специалистом в своей области. Этому способствует и неутолимая потребность в информации.

Квадраты – коллекционеры всевозможных данных. Все сведения систематизированы, разложены по полочкам. Поэтому Квадраты заслуженно слывут эрудитами, по крайней мере, в своей области. Мыслительный анализ – сильная сторона Квадрата. Если вы твердо выбрали для себя Квадрат – фигуру линейную, то, вероятнее всего, вы относитесь к «левополушарным» мыслителям, т.е. к тем, кто перерабатывает данные, говоря языком информатики, в последовательном формате: а-б-в-г и т.д.

Квадраты скорее «вычисляют» результат, чем догадываются о нем. Квадраты чрезвычайно внимательны к деталям, подробностям. Квадраты любят раз и навсегда заведенный порядок. Идеал Квадрата – распланированная, предсказуемая жизнь, и ему не по душе «сюрпризы» и изменения привычного хода событий. Он постоянно «упорядочивает», организует людей и вещи вокруг себя. Все эти качества способствуют тому, что Квадраты могут стать (и становятся!) отличными администраторами, исполнителями, но… увы, редко бывают хорошими распорядителями, менеджерами.

Чрезмерное пристрастие к деталям, потребность в дополнительной, уточняющей информации для принятия решения лишает Квадрата оперативности. Аккуратность, порядок, соблюдение правил и приличий могут развиться до парализующей крайности. И когда приходит время принимать решение, особенно связанное с риском, с возможной потерей статус-кво, Квадраты вольно или невольно затягивают его принятие. Кроме того, рациональность, эмоциональная сухость и холодность мешают Квадратам быстро устанавливать контакты с разными лицами. Квадрат неэффективно действует в аморфной ситуации.

Жизненные ценности: традиции, стабильность, безопасность, надежность, прошлое.

Роли: Консерватор. Надёжа и опора. Педант. Хранитель традиций. Исполнитель.

«Сильные» качества: организованность, дисциплинированность, исполнительность, пунктуальность, аккуратность, чистоплотность, законопослушность, трудолюбие, терпеливость, упорство, настойчивость, верность слову, честность, осторожность, благоразумие, рациональность, бережливость, практичность.

«Слабые» качества: косность, негибкость, инерционность, педантизм, сухость, односторонность, нерешительность, упрямство, консерватизм, сопротивление новому, боязнь риска, бедная фантазия, замкнутость, скупость, мелочность, склонность к бюрократизму.

Внешний вид: опрятный, строгий, неяркий, сдержанный, консервативный, «как положено».

Рабочее место: каждая вещь на своём месте, все «параллельно и перпендикулярно».

Речь: медленная, монотонная, логичная, много опор на авторитеты и на то, «как принято».

Телесные проявления: Позы напряжённые, как правило симметричные. Походка медленная, тяжеловесная, «солидная”. Жестикуляция «небогатая”, но точная. Мимика практически отсутствует — квадрат скуп на проявления чувств.

Подходящие профессии: Бухгалтер, аналитик, заместитель директора по общим или хозяйственным вопросам, участковый инспектор милиции, руководитель в бюрократической организации, «жесткий» секретарь.

Как общаться с квадратом. Выслушивать квадрата до конца, ни в коем случае не перебивать, если вы не его начальник. Быть в глазах квадрата более компетентным, более статусным, чем он. Знать все инструкции, законы, прецеденты. Аргументировать свою позицию, лучше всего фактами и цифрами; очень хорошо использовать таблицы. Делать комплименты – достаточно откровенные, чтобы квадрат их понял (он немного тугодум), но аккуратные, без панибратства и рискованных пассажей. Нововведения предлагать маленькими порциями. Воздерживаться от эмоциональных проявлений.

Форма треугольника символизирует лидерство, и многие Треугольники ощущают в этом свое предназначение. Самая характерная особенность истинного Треугольника – способность концентрироваться на главной цели. Треугольники – энергичные, неудержимые, сильные личности, которые ставят ясные цели и, как правило, достигают их!

Они, как родственники – Квадраты, относятся к линейным формам и в тенденции также являются «левополушарными» мыслителями, способными глубоко и быстро анализировать ситуацию. Однако в противоположность Квадратам, ориентированным на детали, Треугольники сосредотачиваются на главном, на сути проблемы. Их сильная прагматическая ориентация направляет мыслительный анализ и ограничивает его поиском эффективного (и часто эффектного) в данных условиях решения проблемы.

Треугольник – это очень уверенный человек, который хочет быть правым во всем! Сильная потребность быть правым и управлять положением дел, решать не только за себя, но и, по возможности, за других делает Треугольника личностью, постоянно соперничающей, конкурирующей с другими. Доминирующая установка в любом деле – это установка на победу, выигрыш, успех! Он часто рискует, бывает нетерпеливым и нетерпимым к тем, кто колеблется в принятии решений.

Треугольники очень не любят оказываться неправыми и с большим трудом признают свои ошибки, можно сказать, что они видят то, что хотят видеть, поэтому не любят менять свои решения, часто бывают, категоричны, не признают возражений и в большинстве случаев поступят по-своему. Однако они весьма успешно учатся тому, что соответствует их прагматической ориентации, способствует достижению главных целей, и впитывают, как губка, полезную информацию.

Треугольники – честолюбивы. Если делом чести для Квадрата является достижение высшего качества выполн6яемой работы, то Треугольник стремится достичь высокого положения, приобрести высокий статус, иначе говоря – сделать карьеру. Прежде чем взяться за дело или принять решение, Треугольник сознательно или бессознательно ставит перед собой вопрос: «А что я буду с этого иметь?». Из Треугольников получаются великолепные менеджеры на самом «высоком» уровне управления. Они прекрасно умеют представить высшему руководству значимость собственной работы и работы своих подчиненных, за версту чувствуют выгодное дело и в борьбе за него могут «столкнуть лбами» своих противников.

Главное отрицательное качество «треугольной» формы: сильный эгоцентризм, направленность на себя. Треугольники на пути к вершинам власти не проявляют особой щепетильности в отношении моральных норм и могут идти к своей цели по головам других. Это характерно для «завравшихся» Треугольников, которых никто вовремя не остановил. Треугольники заставляют все и всех вращаться вокруг себя, без них жизнь потеряла бы остроту.

Жизненные ценности: власть, лидерство, карьера, статус, победа, будущее.

Роли: Лидер. Пробивной. Воин. Пророк. Герой.

«Сильные» качества: рациональность, эффективность, лидерские качества, энергичность, харизматичность, высокая работоспособность, инициативность, смелость, решительность, независимость суждений.

«Слабые» качества: властность, самоуверенность, эгоизм, категоричность, резкость, язвительность, нетерпимость к инакомыслию, безаппеляционность («или по моему, или никак»), бесчеловечность («пройдет по трупам»).

Внешний вид: в зависимости от обстоятельств: если нужно для дела, то одет броско и «статусно», если нет, то склонен одеваться удобно.

Рабочее место: все в высшей мере функционально, много оргтехники — если позволяют средства, то дорогой, но при этом надежной и удобной.

Речь: быстрая, ясная, четкая, лаконичная, все только «по делу», зачастую «на повышенных тонах» и с использованием сленга и другой «неформальной» лексики.

Телесные проявления: Свободные «широкие» позы. Быстрая, энергичная походка. Уверенные жесты, зачастую похожие на удары. Мимика выразительная, но небогатая.

Подходящие профессии. Руководители в иерархических организациях, в том числе, и высшие, лидеры проектов, врачи-хирурги, психотерапевты «звездного» типа, в особенности гипнотизеры.

Как общаться с треугольником. Говорить только по делу, четко, уверенно, но без «наездов». Договариваться, при этом договора записывать, помнить о том, что все спорные моменты треугольник трактует в свою пользу. Мотивировать выгодой. Можно показать свою власть, но при этом следует быть готовым к «проверке на прочность». Быть готовым со стороны треугольника к шантажу, к обману «ради интересов дела», к присваиванию общих результатов.

Прямоугольник символизирует состояние перехода и изменения. Это временная форма личности, которую могут «носить» остальные четыре сравнительно устойчивые фигуры в определенные периоды жизни. Это – люди, не удовлетворенные тем образом жизни, которые они ведут сейчас, и поэтому заняты поиском лучшего положения.

Причины прямоугольного состояния могут быть самыми различными, но объединяет их одно – значимость изменений для определенного человека. Основным психическим состоянием Прямоугольника является более или менее осознаваемое состояние замешательства, запутанности в проблемах и неопределенности в отношении себя на данный момент времени. Наиболее характерные черты Прямоугольников – непоследовательность и непредсказуемость поступков в течение переходного периода. Прямоугольники могут сильно меняться изо дня в день и даже в пределах одного дня! Они имеют, как правило, низкую самооценку, стремятся стать лучше в чем-то, ищут новые методы работы, стиля жизни. Если внимательно присмотреться к поведению Прямоугольника, то можно заметить, что он применяет в течение всего периода одежду других форм: «треугольную», «круглую» и т. д.

Молниеносные, крутые и непредсказуемые изменения в поведении. Прямоугольники обычно смущают и настораживают других людей, и они могут сознательно уклоняться от контактов с «человеком без стержня». Прямоугольникам общение с другими людьми просто необходимо, и в этом заключается еще одна сложность переходного периода.

Тем не менее, как и у всех людей, у Прямоугольников обнаруживаются позитивные качества, привлекающие к ним окружающих. Это, прежде всего, — любознательность, пытливость, живой интерес ко всему происходящему и … смелость! Прямоугольники пытаются делать то, что никогда раньше не делали; задают вопросы, на что прежде у них не хватало духу. В данный период они открыты для новых идей. Ценностей, способов мышления и жизни, легко усваивают все новое. Правда, оборотной стороной этого является чрезмерная доверчивость, внушаемость, наивность. Поэтому Прямоугольниками легко манипулировать. «Прямоугольность» — всего лишь стадия. Она пройдет!

Жизненные ценности: в зависимости от внешних обстоятельств.

Роли: Размазня. Нерешительный. Козел отпущения. Неудачник. Растяпа.

«Сильные» качества: доверчивость, открытость, чувствительность, любознательность, готовность к изменениям, высокая обучаемость, «детскость», неамбициозность.

«Слабые» качества: наивность, бесхребетность, неуверенность, нерешительность, ненадежность, психическая неустойчивость, «проблемность».

Внешний вид: зачастую неадекватный ситуации, но при этом не экстравагантный, как у зигзага, а в большой степени зависимый от того «что нашлось в гардеробе».

Рабочее место: смесь порядка и беспорядка.

Речь: неуверенная, неясная, сбивчивая, с большими паузами, внезапные непонятные колебания громкости, скорости и высоты тона, «эканье» и «мэканье», ответы вопросом на вопрос.

Телесные проявления: странные, зажатые позы, неуклюжие, резкие движения, неуверенные жесты, дерганная или шаркающая походка, бегающий или стеклянный взгляд.

Подходящие профессии. Поскольку прямоугольник – переходная, зачастую «кризисная» фигура, то лучше всего отправить его на какое-то время в отпуск или на учебу. Идеальное занятие для прямоугольника – эт

Как найти площадь треугольника — Лайфхакер

Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.

Как найти площадь любого треугольника

Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.

Зная сторону и высоту

1. Умножьте сторону треугольника на высоту, проведённую к этой стороне.
2. Поделите результат на два.

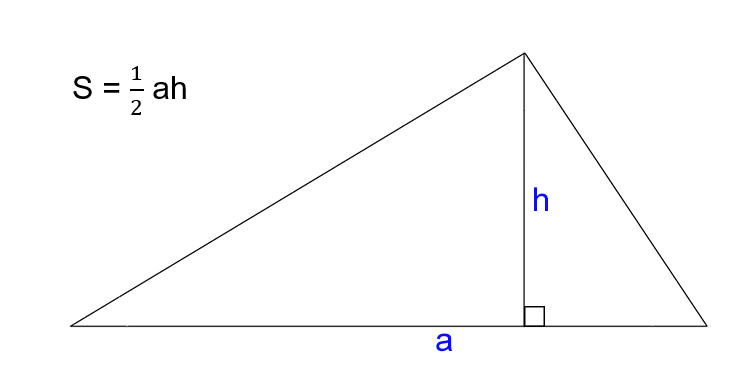
• S — искомая площадь треугольника.
• a — сторона треугольника.
• h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.

Зная две стороны и угол между ними

1. Посчитайте произведение двух известных сторон треугольника.
2. Найдите синус угла между выбранными сторонами.
3. Перемножьте полученные числа.
4. Поделите результат на два.

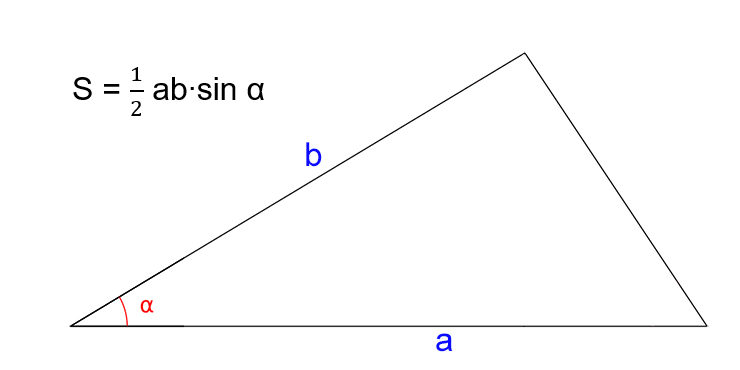
• S — искомая площадь треугольника.
• a и b — стороны треугольника.
• α — угол между сторонами a и b.

Сейчас читают 🔥

Зная три стороны (формула Герона)

1. Посчитайте разности полупериметра треугольника и каждой из его сторон.
2. Найдите произведение полученных чисел.
3. Умножьте результат на полупериметр.
4. Найдите корень из полученного числа.

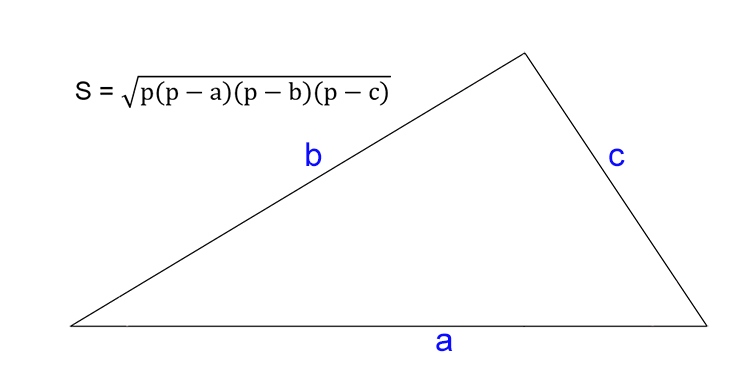
• S — искомая площадь треугольника.
• a, b, c — стороны треугольника.
• p — полупериметр (равен половине от суммы всех сторон треугольника).

Зная три стороны и радиус описанной окружности

1. Найдите произведение всех сторон треугольника.
2. Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.

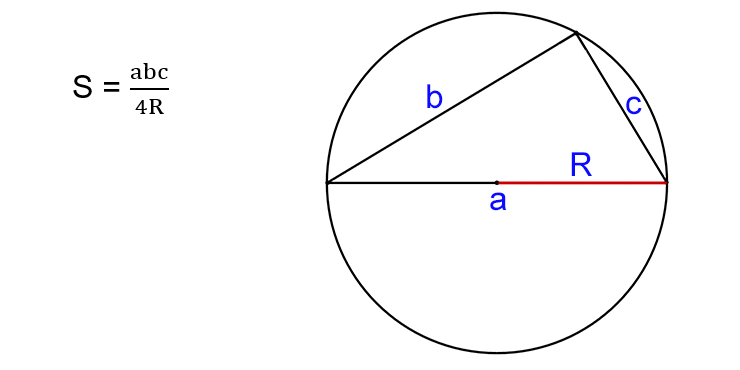
• S — искомая площадь треугольника.
• R — радиус описанной окружности.
• a, b, c — стороны треугольника.

Зная радиус вписанной окружности и полупериметр

Умножьте радиус окружности, вписанной в треугольник, на полупериметр.

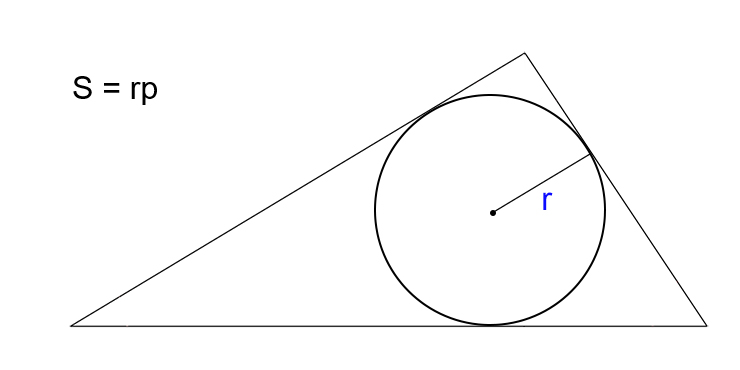
• S — искомая площадь треугольника.
• r — радиус вписанной окружности.
• p — полупериметр треугольника (равен половине от суммы всех сторон).

Как найти площадь прямоугольного треугольника

1. Посчитайте произведение катетов треугольника.
2. Поделите результат на два.

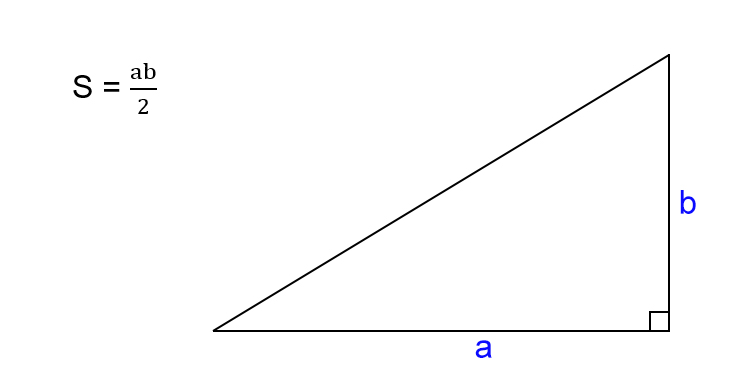
• S — искомая площадь треугольника.
• a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.

Как найти площадь равнобедренного треугольника

1. Умножьте основание на высоту треугольника.
2. Поделите результат на два.

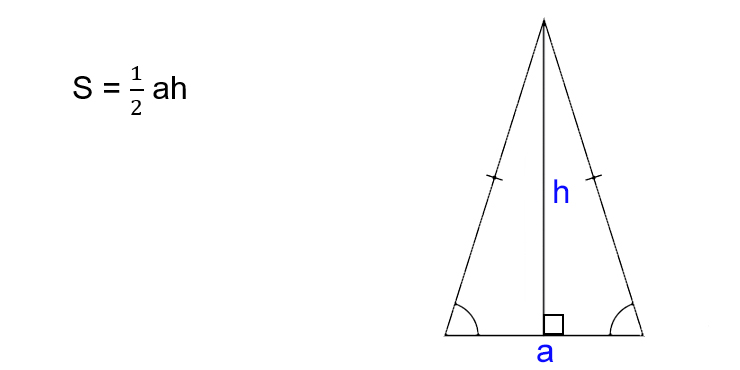
• S — искомая площадь треугольника.
• a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
• h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.

Как найти площадь равностороннего треугольника

1. Умножьте квадрат стороны треугольника на корень из трёх.
2. Поделите результат на четыре.

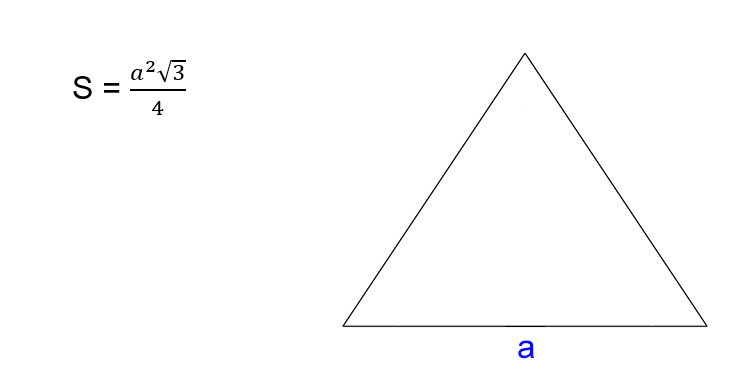
• S — искомая площадь треугольника.
• a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.

Читайте также 🧠👨🏻‍🎓✍🏻

Фигуры вселенной: круг, треугольник, квадрат.

Однажды в одну из суббот мне на ум пришла следующая мысль, что вселенную и все вокруг можно разложить, представить в виде трех фигур. Это удивительная мысль, до конца не известно, откуда родившаяся. Ее произвел мозг, но как она точна. Вероятно долгие годы исследования жизни не прошли зря. Если посмотреть на космос, на прошлое и настоящее, на человека внутри, то,  давайте посмотрим, набором каких фигур можно представить все вокруг.

И, несомненно, когда вселенная задумывалась, то легче всего было представить ее каждый элемент в виде комбинаций нескольких простых фигур и этими тремя фигурами являются круг, треугольник и квадрат. Возьмем солнце, на что оно похоже? Верно, на круг. А земля? Тоже на круг. Монитор можно представить в виде множества квадратов, пиксель также квадрат, глаз рыбы – это круг. А ядро клетки и молекула ДНК – сложнейшие невообразимые структуры генетической информации, и те при рассмотрении под микроскопом напоминают нам все те же фигуры.

Любые дома чаще всего это квадраты и треугольники. Автомобиль, самолет, ракета, катер, любая техника – это все тоже множество фигур. Телевизор, который все смотрят и всеми любимый айпад с айфоном также прямоугольники, а любой прямоугольник можно представить в виде множества квадратов. Фотографии, картинки, баннеры – это множество квадратов. Провода окутали весь земной шар, а в разрезе это все те же окружности. А свет, волны, электроны, протоны, молекулы, микробы, которые нас окружают, они состоят также из более мелких частиц, которые в свою очередь можно представить в виде кругов. Одни из самых загадочных пирамид – в Египте. Люди до конца не знаю, кто их построил. Если на них посмотреть в разрезе, то мы увидим множество треугольников.

 

В искусстве очень много примеров, когда художники изображают элементы мира, чувства, эмоции, людей, и даже сюжеты библии в виде геометрических фигур. В спорте мяч имеет округлую форму, а поле для игры чаще всего прямоугольную. И любую сложную фигуру всегда можно разбить на несколько простых. Мысль о трех фигурах не останавливалась только на структуре материального и видимого мира, она также относится и к строению тонкой материи. Между людьми, животными, растениями и живыми существами существуют тонкие связи и их также можно представить в виде геометрии связей. К примеру, человек А знает человека Б, человек Б знает человека С, когда человек А знакомится также с человеком С, то образуется сильный треугольник. Причем не важно, где находятся люди, в каких городах и странах мира.

В треугольнике и образуется самая сильная связь, энергия. Несомненно, поэтому на земле самое популярное количество семей, которых состоят из трех человек. Энергия остальных фигур менее устойчива, так как большое количество людей продолжительное время, вероятно, не могут быть вместе, сложнее поддерживать отношения между всеми членами. Отношения и люди с годами, как известно, меняются. И вот мир весь пронизан такими тонкими связями. Наверно, поэтому, иногда хочется верить, что мысли материальны и передаются они от человека к человеку именно путем таких тонких геометрических связей.

Автор: Трепольский Дмитрий

Теорема Пифагора — Википедия

Схема, объясняющая доказательство теоремы Пифагора через равнодополняемость^[⇨]

Теоре́ма Пифаго́ра — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.

Соотношение в том или ином виде предположительно было известно различным древним цивилизациям задолго до нашей эры; первое геометрическое доказательство приписывается Пифагору. Утверждение появляется как Предложение 47 в «Началах» Евклида^[⇨].

Также может быть выражена как геометрический факт о том, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Верно и обратное утверждение^[⇨]: треугольник, сумма квадратов длин двух сторон которого равна квадрату длины третьей стороны, является прямоугольным.

Существует ряд обобщений данной теоремы^[⇨] — для произвольных треугольников, для фигур в пространствах высших размерностей. В неевклидовых геометриях теорема не выполняется^[⇨].

По мнению историка математики Морица Кантора, в Древнем Египте во времена царя Аменемхета I (около XXIII век до н. э.) было известно о прямоугольном треугольнике со сторонами 3, 4, 5 — его использовали гарпедонапты — «натягиватели верёвок»^[1]. В древневавилонском тексте, относимом ко временам Хаммурапи (XX век до н. э.), приведено приближённое вычисление гипотенузы^[2]. По мнению Ван-дер-Вардена, очень вероятно, что соотношение в общем виде было известно в Вавилоне уже около XVIII века до н. э.

В древнекитайской книге «Чжоу би суань цзин», относимой к периоду V—III веков до н. э., приводится треугольник со сторонами 3, 4 и 5, притом изображение можно трактовать как графическое обоснование соотношения теоремы^[3]. В китайском сборнике задач «Математика в девяти книгах» (X—II веков до н. э.) применению теоремы посвящена отдельная книга.

Общепринято, что доказательство соотношения дано древнегреческим философом Пифагором (570—490 до н. э.). Имеется свидетельство Прокла (412—485 н. э.), что Пифагор использовал алгебраические методы, чтобы находить пифагоровы тройки^[⇨][4], но при этом в течение пяти веков после смерти Пифагора прямых упоминаний о доказательстве его авторства не находится. Однако когда такие авторы, как Плутарх и Цицерон, пишут о теореме Пифагора, из содержания следует, будто авторство Пифагора общеизвестно и несомненно^[5][6]. Существует предание, сообщённое Диогеном Лаэртским, согласно которому Пифагор якобы отпраздновал открытие своей теоремы гигантским пиром, заклав на радостях сотню быков^[7].

Приблизительно в 400 году до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Около 300 года до н. э. в «Началах» Евклида появилось старейшее аксиоматическое доказательство теоремы Пифагора^[8].

Сумма площадей квадратов, опирающихся на катеты a{\displaystyle a} и b{\displaystyle b}, равна площади квадрата, построенного на гипотенузе c{\displaystyle c}

Основная формулировка содержит алгебраические действия — в прямоугольном треугольнике, длины катетов которого равны a{\displaystyle a} и b{\displaystyle b}, а длина гипотенузы — c{\displaystyle c}, выполнено соотношение:

a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}}.

Возможна и эквивалентная геометрическая формулировка, прибегающая к понятию площади фигуры: в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. В таком виде теорема сформулирована в Началах Евклида.

Обратная теорема Пифагора — утверждение о прямоугольности всякого треугольника, длины сторон которого связаны соотношением a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}}. Как следствие, для всякой тройки положительных чисел a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c}, такой, что a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}}, существует прямоугольный треугольник с катетами a{\displaystyle a} и b{\displaystyle b} и гипотенузой c{\displaystyle c}.

В научной литературе зафиксировано не менее 400 доказательств теоремы Пифагора^[9], что объясняется как фундаментальным значением для геометрии, так и элементарностью результата. Основные направления доказательств: алгебраическое использование соотношений элементов треугольника (таков, например, популярный метод подобия^[⇨]), метод площадей^[⇨], существуют также различные экзотические доказательства (например, с помощью дифференциальных уравнений).

Через подобные треугольники[править | править код]

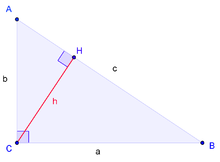
Одним из наиболее популярных в учебной литературе доказательств алгебраической формулировки является доказательство с использованием техники подобия треугольников, при этом оно почти непосредственно выводится из аксиом и не задействует понятие площади фигуры. В нём для треугольника △ABC{\displaystyle \triangle ABC} с прямым углом при вершине C{\displaystyle C} со сторонами a,b,c{\displaystyle a,b,c}, противолежащими вершинам A,B,C{\displaystyle A,B,C} соответственно, проводится высота CH{\displaystyle CH}, при этом (согласно признаку подобия по равенству двух углов) возникают соотношения подобия: △ABC∼△ACH{\displaystyle \triangle ABC\sim \triangle ACH} и △ABC∼△CBH{\displaystyle \triangle ABC\sim \triangle CBH}, из чего непосредственно следуют соотношения:

ac=|HB|a{\displaystyle {\frac {a}{c}}={\frac {|HB|}{a}}}; bc=|AH|b{\displaystyle {\frac {b}{c}}={\frac {|AH|}{b}}}.

При перемножении крайних членов пропорций выводятся равенства:

a2=c⋅|HB|{\displaystyle a^{2}=c\cdot |HB|}; b2=c⋅|AH|{\displaystyle b^{2}=c\cdot |AH|},

покомпонентное сложение которых даёт требуемый результат:

a2+b2=c⋅(|HB|+|AH|)=c2⇔a2+b2=c2{\displaystyle a^{2}+b^{2}=c\cdot \left(|HB|+|AH|\right)=c^{2}\,\Leftrightarrow \,a^{2}+b^{2}=c^{2}}.

Доказательства методом площадей[править | править код]

Большое число доказательств задействуют понятие площади. Несмотря на видимую простоту многих из них, такие доказательства используют свойства площадей фигур, доказательства которых сложнее доказательства самой теоремы Пифагора.

Доказательство через равнодополняемость[править | править код]

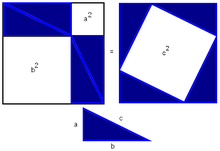Схема доказательства через равнодополняемость.

Доказательство через равнодополняемость использует четыре копии прямоугольного треугольника с катетами a,b{\displaystyle a,b} и гипотенузой c{\displaystyle c}, расположенные таким образом, чтобы образовывать квадрат со стороной a+b{\displaystyle a+b} и внутренний четырёхугольник со сторонами длиной c{\displaystyle c}. Внутренний четырёхугольник в этой конфигурации является квадратом, так как сумма двух противоположных прямому острых углов — 90°, а развёрнутый угол — 180°. Площадь внешнего квадрата равна (a+b)2{\displaystyle (a+b)^{2}}, он состоит из внутреннего квадрата площадью c2{\displaystyle c^{2}} и четырёх прямоугольных треугольников, каждый площадью ab2{\displaystyle {\frac {ab}{2}}}, в результате из соотношения (a+b)2=4⋅ab2+c2{\displaystyle (a+b)^{2}=4\cdot {\frac {ab}{2}}+c^{2}} при алгебраическом преобразовании следует утверждение теоремы.

Доказательство Евклида[править | править код]

Чертёж к доказательству Евклида. Основное направление доказательства — установление конгруэнтности △ACK≅△ABD{\displaystyle \triangle ACK\cong \triangle ABD}, площадь которых составляет половину площади прямоугольников AHJK{\displaystyle AHJK} и ACED{\displaystyle ACED} соответственно.

Классическое доказательство Евклида направлено на установление равенства площадей между прямоугольниками, образованными из рассечения квадрата над гипотенузой высотой из прямого угла с квадратами над катетами.

Конструкция, используемая для доказательства следующая: для прямоугольного треугольника △ABC{\displaystyle \triangle ABC} с прямым углом C{\displaystyle C}, квадратов над катетами ACED{\displaystyle ACED} и BCFG{\displaystyle BCFG} и квадрата над гипотенузой ABIK{\displaystyle ABIK} строится высота CH{\displaystyle CH} и продолжающий её луч s{\displaystyle s}, разбивающий квадрат над гипотенузой на два прямоугольника AHJK{\displaystyle AHJK} и BHJI{\displaystyle BHJI}. Доказательство нацелено на установление равенства площадей прямоугольника AHJK{\displaystyle AHJK} с квадратом над катетом AC{\displaystyle AC}; равенство площадей второго прямоугольника, составляющего квадрат над гипотенузой, и прямоугольника над другим катетом устанавливается аналогичным образом.

Равенство площадей прямоугольника AHJK{\displaystyle AHJK} и ACED{\displaystyle ACED} устанавливается через конгруэнтность треугольников △ACK{\displaystyle \triangle ACK} и △ABD{\displaystyle \triangle ABD}, площадь каждого из которых равна половине площади прямоугольников AHJK{\displaystyle AHJK} и ACED{\displaystyle ACED} соответственно в связи со следующим свойством: площадь треугольника равна половине площади прямоугольника, если у фигур есть общая сторона, а высота треугольника к общей стороне является другой стороной прямоугольника. Конгруэнтность треугольников следует из равенства двух сторон (стороны квадратов) и углу между ними (составленного из прямого угла и угла при A{\displaystyle A}).

Таким образом, доказательством устанавливается, что площадь квадрата над гипотенузой, составленного из прямоугольников AHJK{\displaystyle AHJK} и BHJI{\displaystyle BHJI}, равна сумме площадей квадратов над катетами.

Доказательство Леонардо да Винчи[править | править код]

Чертёж к доказательству Леонардо да Винчи

К методу площадей относится также доказательство, найденное Леонардо да Винчи. Пусть дан прямоугольный треугольник △ABC{\displaystyle \triangle ABC} с прямым углом C{\displaystyle C} и квадраты ACED{\displaystyle ACED}, BCFG{\displaystyle BCFG} и ABHJ{\displaystyle ABHJ} (см. рисунок). В этом доказательстве на стороне HJ{\displaystyle HJ} последнего во внешнюю сторону строится треугольник, конгруэнтный △ABC{\displaystyle \triangle ABC}, притом отражённый как относительно гипотенузы, так и относительно высоты к ней (то есть JI=BC{\displaystyle JI=BC} и HI=AC{\displaystyle HI=AC}). Прямая CI{\displaystyle CI} разбивает квадрат, построенный на гипотенузе на две равные части, поскольку треугольники △ABC{\displaystyle \triangle ABC} и △JHI{\displaystyle \triangle JHI} равны по построению. Доказательство устанавливает конгруэнтность четырёхугольников CAJI{\displaystyle CAJI} и DABG{\displaystyle DABG}, площадь каждого из которых, оказывается, с одной стороны, равной сумме половин площадей квадратов на катетах и площади исходного треугольника, с другой стороны — половине площади квадрата на гипотенузе плюс площадь исходного треугольника. Итого, половина суммы площадей квадратов над катетами равна половине площади квадрата над гипотенузой, что равносильно геометрической формулировке теоремы Пифагора.

Через площади подобных треугольников[править | править код]

Следующее доказательство основано на том, что площади подобных треугольников относятся как квадраты соответственных сторон.

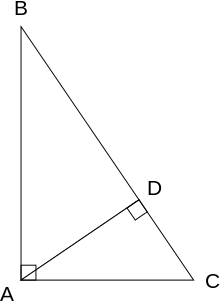
Пусть ABC{\displaystyle ABC} есть прямоугольный треугольник, AD{\displaystyle AD} — перпендикуляр, опущенный на гипотенузу из вершины прямого угла. Треугольники ABC{\displaystyle ABC}, DBA{\displaystyle DBA} подобны, так как имеют по прямому углу и ещё общий угол B{\displaystyle B}. Значит

площадь DBAплощадь ABC=AB2BC2.{\displaystyle {\frac {{\text{площадь}}~DBA}{{\text{площадь}}~ABC}}={\frac {AB^{2}}{BC^{2}}}.}

Точно также получаем, что

площадь DACплощадь ABC=AC2BC2.{\displaystyle {\frac {{\text{площадь}}~DAC}{{\text{площадь}}~ABC}}={\frac {AC^{2}}{BC^{2}}}.}

Поскольку треугольники DBA{\displaystyle DBA} и DAC{\displaystyle DAC} вместе составляют △ABC{\displaystyle \triangle ABC}, сумма площадей △DBA{\displaystyle \triangle DBA} и △DAC{\displaystyle \triangle DAC} равна площади △ABC{\displaystyle \triangle ABC}. Отсюда

AB2+AC2BC2=1{\displaystyle {\frac {AB^{2}+AC^{2}}{BC^{2}}}=1}

или AB2+AC2=BC2.{\displaystyle AB^{2}+AC^{2}=BC^{2}.}

Доказательство методом бесконечно малых[править | править код]

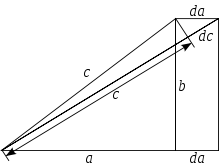Доказательство методом бесконечно малых

Существует несколько доказательств, прибегающих к технике дифференциальных уравнений. В частности, Харди приписывается доказательство, использующее бесконечно малые приращения катетов a{\displaystyle a} и b{\displaystyle b} и гипотенузы c{\displaystyle c}. Например, приращение катета da{\displaystyle da} при постоянном катете b{\displaystyle b} приводит к приращению гипотенузы dc{\displaystyle dc}, так что

dadc=ca{\displaystyle {\frac {da}{dc}}={\frac {c}{a}}}

Методом разделения переменных из них выводится дифференциальное уравнение c dc=ada{\displaystyle c\ dc=a\,da}, интегрирование которого даёт соотношение c2=a2+Const{\displaystyle c^{2}=a^{2}+\mathrm {Const} }. Применение начальных условий a=0,c=b{\displaystyle a=0,c=b} определяет константу как b2{\displaystyle b^{2}}, что в результате даёт утверждение теоремы.

Квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.

Подобные геометрические фигуры на трёх сторонах[править | править код]

Обобщение для подобных треугольников, сумма площадей зелёных фигур равна площади синей Теорема Пифагора с использованием подобных прямоугольных треугольников

Важное геометрическое обобщение теоремы Пифагора дал Евклид в «Началах», перейдя от площадей квадратов на сторонах к площадям произвольных подобных геометрических фигур^[10]: сумма площадей таких ф

Исчезновение клетки — Википедия

Исчезновение клетки (появление клетки) — известный класс задач (оптических иллюзий) на перестановку фигур, обладающих признаками математических софизмов: изначально в их условие введена замаскированная ошибка. Некоторые из этих задач тесно связаны со свойствами последовательности чисел Фибоначчи.

1 Перестановка частей 2 Разрезанный треугольник

Дан прямоугольный треугольник 13×5 клеток, составленный из 4 частей. После перестановки частей при визуальном сохранении изначальных пропорций появляется дополнительная, не занятая ни одной частью, клетка (рисунок 1).

Решение[править | править код]

3 «Гипотенуза» на самом деле является ломаной линией

Площади закрашенных фигур, разумеется, равны между собой (32 клетки), однако, то, что визуально наблюдается как треугольники 13×5, на самом деле таковым не является, и имеет разные площади (S_13×5 = 32,5 клетки). То есть ошибка, замаскированная в условии задачи, состоит в том, что начальная фигура поименована треугольником (на самом деле это — вогнутый 4-угольник). Это отчётливо заметно на рисунках 2 и 3 — «гипотенузы» верхней и нижней фигур проходят через разные точки: (8,3) вверху и (5,2) — внизу. Секрет в свойствах синего и красного треугольников. Это легко проверить вычислениями.

Отношения длин соответствующих сторон синего и красного треугольников не равны друг другу (2/3 и 5/8), поэтому эти треугольники не являются подобными, а значит, имеют разные углы при соответствующих вершинах. Назовём первую фигуру, являющуюся вогнутым четырёхугольником, и вторую фигуру, являющуюся вогнутым восьмиугольником, псевдотреугольниками. Если нижние стороны этих псевдотреугольников параллельны, то гипотенузы в обоих псевдотреугольниках 13×5 на самом деле являются ломаными линиями (на верхнем рисунке создаётся излом внутрь, а на нижнем — наружу). Если наложить верхнюю и нижнюю фигуры 13×5 друг на друга, то между их «гипотенузами» образуется параллелограмм, в котором и содержится «лишняя» площадь. На рисунке 3 этот параллелограмм приведён в верных пропорциях.

Острый угол в этом параллелограмме равен arcctg 46^[1] ≈ 0°1′18,2″. На такой угол минутная стрелка на исправных часах сдвигается за 12,45 с. Именно на такую величину тупой угол в рассматриваемом параллелограмме отличается от развёрнутого. Визуально столь ничтожное отличие незаметно.

По словам Мартина Гарднера, эту задачу изобрёл иллюзионист-любитель из Нью-Йорка Пол Карри в 1953. Однако принцип, заложенный в неё, был известен ещё в 1860-е годы. Можно заметить, что длины сторон фигур из данной задачи (2, 3, 5, 8, 13) являются последовательными числами Фибоначчи.

Маленький квадрат «исчезает» и «появляется» при повороте частей

В другой похожей головоломке, большой квадрат составлен из четырёх одинаковых четырёхугольников^[2] и маленького квадрата. Если четырёхугольники развернуть, то они заполнят площадь, занимаемую маленьким квадратом, хотя площадь большого квадрата визуально не изменится. При следующем развороте маленький квадрат появится снова.

Решение[править | править код]

Этот парадокс объясняется тем, что сторона (и площадь) нового большого квадрата немного отличается от стороны́ (и площади) того, который был в начале. Если в качестве первой фигуры принять тот квадрат, в середине которого нет маленького ромба, дальнейший анализ заметно упростится.

Сторона начального квадрата пусть будет α{\displaystyle \alpha }, и сто́роны составляющих его четырёхугольников делят эту сто́рону (α{\displaystyle \alpha }) в отношении κ (1/2<κ<1){\displaystyle \kappa \ \,(1/2<\kappa <1)}. Сведущий в геометрии легко сможет доказать, что построенные таким образом четырёхугольники равны друг другу, имеют прямые углы в противолежащих вершинах (в центре и по углам квадрата) и равные стороны, смежные в центре квадрата (то есть не являются ромбоидами + для них существуют описанные окружности (суммы противолежащих углов равны^[3])). Становится также понятно, что ромб в центре второй фигуры является квадратом.

Сторона маленького квадрата на второй фигуре будет равна α(2κ−1){\displaystyle \alpha (2\kappa -1)}. Угол между парой противоположных сторон любого из составляющих четырёхугольников (причём, не важно, какой парой) пусть будет обозначен θ{\displaystyle \theta }. Его точное значение можно рассчитать^[4] методом координат, или методами классической геометрии.

Если каждый из четырёхугольников, составляющих первый квадрат, повернуть на угол π{\displaystyle \pi } вокруг центра описанной около него окружности, то получится вторая фигура, с незакрашенной квадратной областью в центре. При следующем повороте опять составится первый квадрат. Площадь второго квадрата оказывается в (4κ(κ−1)+2){\displaystyle (4\kappa (\kappa -1)+2)} раза больше площади первого (или, что то же, в sec2⁡θ{\displaystyle \sec ^{2}\theta } раз). При κ≈1/2{\displaystyle \kappa \approx 1/2} это отличие практически незаметно. Например, на поясняющих рисунках использован угол θ=10∘{\displaystyle \theta =10^{\circ }} (соответственно, κ=(tgθ+1)/2≈0,5882{\displaystyle \kappa =(\mathrm {tg} \,\theta +1)/2\approx 0,588\,2}). При этом разность между площадями больши́х квадратов составляет ≈3,11%{\displaystyle \approx 3{,}11\,\%}. Уже такое отличие сложно заметить, хотя значение κ{\displaystyle \kappa } (и, соответственно, значение угла θ{\displaystyle \theta }) здесь используется отнюдь не маленькое.

Таким образом, можно заключить, что ошибка, замаскированная в условии, состоит в том, что центры вращения составляющих четырёхугольников находятся не там, где это представляется при визуальном контроле картинки (не в точках пересечения их диагоналей). Они находятся в вершинах квадрата, повёрнутого на угол −θ{\displaystyle -\theta } относительно первого квадрата, хотя его стороны параллельны сторонам второго.

1. ↑ Меньший угол в прямоугольном треугольнике с соотношением катетов 1/46.
2. ↑ Из рисунка видно, что соответствующие стороны у них равны. Из этого следует, что средняя фигура, как минимум, ромб.
3. ↑ равны π{\displaystyle \pi }, хотя для выпуклого четырёхугольника это несущественное замечание
4. ↑ θ=arcsec(4(κ−1)κ+2){\displaystyle \theta =\mathrm {arcsec} \left({\sqrt {4(\kappa -1)\kappa +2}}\right)}, причём под корнем здесь — отношение площадей больши́х квадратов (второго к первому).

Треугольник Рёло — Википедия

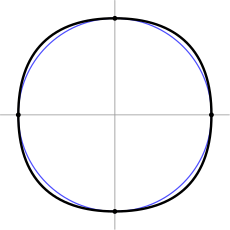
Построение треугольника Рёло

Треуго́льник Рёло́^{[* 1]} представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне^[1][2]. Негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло.

Треугольник Рёло является простейшей после круга фигурой постоянной ширины^[1]. То есть если к треугольнику Рёло провести пару параллельных опорных прямых^{[* 2]}, то расстояние между ними не будет зависеть от выбранного направления^[3]. Это расстояние называется шириной треугольника Рёло.

Среди прочих фигур постоянной ширины треугольник Рёло выделяется рядом экстремальных свойств: наименьшей площадью^[1], наименьшим возможным углом при вершине^[4], наименьшей симметричностью относительно центра^[5]. Треугольник получил распространение в технике — на его основе были созданы кулачковые и грейферные механизмы, роторно-поршневой двигатель Ванкеля и даже дрели, позволяющие сверлить (фрезеровать) квадратные отверстия^[6].

Название фигуры происходит от фамилии немецкого механика Франца Рёло. Он, вероятно, был первым, кто исследовал свойства этого так называемого криволинейного треугольника; также он использовал его в своих механизмах^[7].

Рёло не является первооткрывателем этой фигуры, хотя он и подробно исследовал её. В частности, он рассматривал вопрос о том, сколько контактов (в кинематических парах) необходимо, чтобы предотвратить движение плоской фигуры, и на примере искривлённого треугольника, вписанного в квадрат, показал, что даже трёх контактов может быть недостаточно для того, чтобы фигура не вращалась^[8].

Некоторые математики считают, что первым продемонстрировал идею треугольника из равных дуг окружности Леонард Эйлер в XVIII веке^[9]. Тем не менее, подобная фигура встречается и раньше, в XV веке: её использовал в своих рукописях Леонардо да Винчи. Треугольник Рёло есть в его манускриптах A и B, хранящихся в Институте Франции^[10], а также в Мадридском кодексе^[9].

Примерно в 1514 году Леонардо да Винчи создал одну из первых в своём роде карт мира. Поверхность земного шара на ней была разделена экватором и двумя меридианами (угол между плоскостями этих меридианов равен 90°) на восемь сферических треугольников, которые были показаны на плоскости карты треугольниками Рёло, собранными по четыре вокруг полюсов^[11].

Ещё раньше, в XIII веке, создатели церкви Богоматери в Брюгге использовали треугольник Рёло в качестве формы для некоторых окон^[9].

Треугольник Рёло является плоской выпуклой геометрической фигурой^[12].

Основные геометрические характеристики[править | править код]

Если ширина треугольника Рёло равна a{\displaystyle a}, то его площадь равна^[13]

S=12(π−3)⋅a2,{\displaystyle S={{1} \over {2}}\left(\pi -{\sqrt {3}}\right)\cdot a^{2},}

периметр

p=πa,{\displaystyle p=\pi a,}

радиус вписанной окружности

r=(1−13)⋅a,{\displaystyle r=\left(1-{{1} \over {\sqrt {3}}}\right)\cdot a,}

а радиус описанной окружности

R=a3{\displaystyle R={{a} \over {\sqrt {3}}}}.

Симметрия[править | править код]

Треугольник Рёло обладает осевой симметрией. Он имеет три оси симметрии второго порядка, каждая из которых проходит через вершину треугольника и середину противоположной дуги, а также одну ось симметрии третьего порядка, перпендикулярную плоскости треугольника и проходящую через его центр^{[* 3]}. Таким образом, группа симметрий треугольника Рёло состоит из шести отображений (включая тождественное) и совпадает с группой D3{\displaystyle D_{3}} симметрий правильного треугольника.

Построение циркулем[править | править код]

Треугольник Рёло можно построить с помощью одного только циркуля, не прибегая к линейке. Это построение сводится к последовательному проведению трёх равных окружностей. Центр первой выбирается произвольно, центром второй может быть любая точка первой окружности, а центром третьей — любая из двух точек пересечения первых двух окружностей.

Свойства, общие для всех фигур постоянной ширины[править | править код]

Поскольку треугольник Рёло является фигурой постоянной ширины, он обладает всеми общими свойствами фигур этого класса. В частности,

• с каждой из своих опорных прямых треугольник Рёло имеет лишь по одной общей точке^[14];
• расстояние между двумя любыми точками треугольника Рёло ширины a{\displaystyle a} не может превышать a{\displaystyle a}^[15];
• отрезок, соединяющий точки касания двух параллельных опорных прямых к треугольнику Рёло, перпендикулярен к этим опорным прямым^[16];
• через любую точку границы треугольника Рёло проходит по крайней мере одна опорная прямая^[17];
• через каждую точку P{\displaystyle P} границы треугольника Рёло проходит объемлющая его окружность радиуса a{\displaystyle a}^{[* 4]}, причём опорная прямая, проведённая к треугольнику Рёло через точку P{\displaystyle P}, является касательной к этой окружности^[18];
• радиус окружности, имеющей не меньше трёх общих точек с границей треугольника Рёло ширины a{\displaystyle a}, не превышает a{\displaystyle a}^[19];
• по теореме Ханфрида Ленца^[de] о множествах постоянной ширины треугольник Рёло нельзя разделить на две фигуры, диаметр которых был бы меньше ширины самого треугольника^[20][21];
• треугольник Рёло, как и любую другую фигуру постоянной ширины, можно вписать в квадрат^[22], а также в правильный шестиугольник^[23];
• по теореме Барбье формула периметра треугольника Рёло справедлива для всех фигур постоянной ширины^[24][25][26].

Экстремальные свойства[править | править код]

Наименьшая площадь[править | править код]

Среди всех фигур постоянной ширины a{\displaystyle a} у треугольника Рёло наименьшая площадь^[1]. Это утверждение носит название теоремы Бляшке — Лебега^[27][28] (по фамилиям немецкого геометра Вильгельма Бляшке, опубликовавшего теорему в 1915 году^[29], и французского математика Анри Лебега, который сформулировал её в 1914 году^[30]). В разное время варианты её доказательства предлагали Мацусабуро Фудзивара (1927 и 1931 год)^[31][32], Антон Майер (1935 год)^[33], Гарольд Эгглстон (1952 год)^[34], Абрам Безикович (1963 год)^[35], Дональд Чакериан (1966 год)^[36], Эванс Харрелл (2002 год)^[37] и другие математики^[5].

Чтобы найти площадь треугольника Рёло, можно сложить площадь внутреннего равностороннего треугольника

S△=34⋅a2{\displaystyle S_{\triangle }={{\sqrt {3}} \over {4}}\cdot a^{2}}

и площадь трёх оставшихся одинаковых круговых сегментов, опирающихся на угол в 60°

Sseg=a22(π3−sin⁡π3)=(π6−34)⋅a2,{\displaystyle S_{seg}={{a^{2}} \over {2}}\left({{\pi } \over {3}}-\sin {{\pi } \over {3}}\right)={\left({{\pi } \over {6}}-{{\sqrt {3}} \over {4}}\right)\cdot a^{2}},}

то есть

Srt=S△+3Sseg=12(π−3)⋅a2=a2⋅0,70477…{\displaystyle S_{rt}=S_{\triangle }+3S_{seg}={{1} \over {2}}\left(\pi -{\sqrt {3}}\right)\cdot a^{2}=a^{2}\cdot 0{,}70477\ldots }^[38]

Фигура, обладающая противоположным экстремальным свойством — круг. Среди всех фигур данной постоянной ширины его площадь

S◯=a2⋅π4=a2⋅0,78539…{\displaystyle S_{\bigcirc }=a^{2}\cdot {{\pi } \over {4}}=a^{2}\cdot 0{,}78539\ldots }

максимальна^{[39][* 5]}. Площадь соответствующего треугольника Рёло меньше на ≈10,27 %. В этих пределах лежат площади всех остальных фигур данной постоянной ширины.

Наименьший угол[править | править код]

Через каждую вершину треугольника Рёло, в отличие от остальных его граничных точек, проходит не одна опорная прямая, а бесконечное множество опорных прямых. Пересекаясь в вершине, они образуют «пучок». Угол между крайними прямыми этого «пучка» называется углом при вершине. Для фигур постоянной ширины угол при вершинах не может быть меньше 120°. Единственная фигура постоянной ширины, имеющая углы, равные в точности 120° — это треугольник Рёло^[4].

Наименьшая центральная симметрия[править | править код]

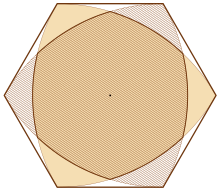Треугольник Рёло (бежевый) и его образ при центральной симметрии относительно своего центра (заштрихован). Наибольшая центрально-симметричная фигура, в нём содержащаяся (криволинейный шестиугольник), и наименьшая центрально-симметричная выпуклая, его содержащая (правильный шестиугольник) выделены жирной линией

Из всех фигур постоянной ширины треугольник Рёло обладает центральной симметрией в наименьшей степени^{[5][40][41][42][43]}. Существует несколько различных способов дать определение степени симметричности фигуры. Один из них — это мера Ковнера — Безиковича. В общем случае для выпуклой фигуры C{\displaystyle C} она равна

σ(C)=μ(A)μ(C),{\displaystyle \sigma (C)={{\mu (A)} \over {\mu (C)}},}

где μ{\displaystyle \mu } — площадь фигуры, A{\displaystyle A} — содержащаяся в C{\displaystyle C} центрально-симметричная выпуклая фигура максимальной площади. Для треугольника Рёло такой фигурой является шестиугольник с искривлёнными сторонами, представляющий собой пересечение этого треугольника Рёло со своим образом при центральной симметрии относительно своего центра^{[* 3]}. Мера Ковнера — Безиковича для треугольника Рёло равна

σ=6arccos⁡(5+3312)+3−11π−3=0,84034…{\displaystyle \sigma ={{6\arccos {\left({{5+{\sqrt {33}}} \over {12}}\right)}+{\sqrt {3}}-{\sqrt {11}}} \over {\pi -{\sqrt {3}}}}=0{,}84034\ldots }^[5][40]

Другой способ — это мера Эстерманна

τ(C)=μ(C)μ(B),{\displaystyle \tau (C)={{\mu (C)} \over {\mu (B)}},}

где B{\displaystyle B} — содержащая C{\displaystyle C} центрально-симметричная фигура минимальной площади. Для треугольника Рёло B{\displaystyle B} — это правильный шестиугольник, поэтому мера Эстерманна равна

τ=π−33=0,81379…{\displaystyle \tau ={{\pi -{\sqrt {3}}} \over {\sqrt {3}}}=0{,}81379\ldots }^[5][36]

Для центрально-симметричных фигур меры Ковнера — Безиковича и Эстерманна равны единице. Среди фигур постоянной ширины центральной симметрией обладает только круг^[25], который (вместе с треугольником Рёло) и ограничивает область возможных значений их симметричности.

Качение по квадрату[править | править код]

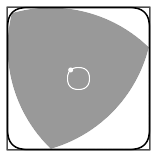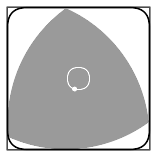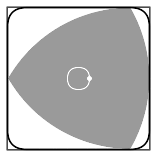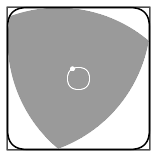
Любая фигура постоянной ширины вписана в квадрат со стороной, равной ширине фигуры, причём направление сторон квадрата может быть выбрано произвольно^{[22][* 6]}. Треугольник Рёло — не исключение, он вписан в квадрат и может вращаться в нём, постоянно касаясь всех четырёх сторон^[44].

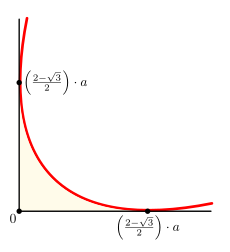
Каждая вершина треугольника при его вращении «проходит» почти весь периметр квадрата, отклоняясь от этой траектории лишь в углах — там вершина описывает дугу эллипса. Центр этого эллипса расположен в противоположном углу квадрата, а его больша́я и малая оси повёрнуты на угол в 45° относительно сторон квадрата и равны

a⋅(3±1),{\displaystyle a\cdot \left({\sqrt {3}}\pm 1\right),}

где a{\displaystyle a} — ширина треугольника^[45]. Каждый из четырёх эллипсов касается двух смежных сторон квадрата на расстоянии

a⋅(1−32)=a⋅0,13397…{\displaystyle a\cdot \left(1-{{\sqrt {3}} \over {2}}\right)=a\cdot 0{,}13397\ldots }

от угла^[38].

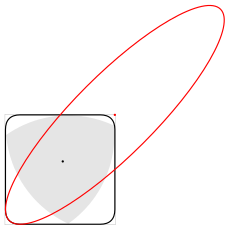Эллипс (выделен красным цветом), очерчивающий один из углов фигуры (её граница выделена чёрным цветом), которую покрывает треугольник Рёло при вращении в квадрате	Угол покрываемой вращением фигуры. Подписаны точки касания сторон квадрата с эллипсом. Светло-жёлтым показан не затронутый вращением угол квадрата

Центр треугольника Рёло при вращении движется по траектории, составленной из четырёх одинаковых дуг эллипсов. Центры этих эллипсов расположены в вершинах квадрата, а оси повёрнуты на угол в 45° относительно сторон квадрата и равны

a⋅(1±13){\displaystyle a\cdot \left(1\pm {{1} \over {\sqrt {3}}}\right)}^[45].

Иногда для механизмов, реализующих на практике такое вращение треугольника, в качестве траектории центра выбирают не склейку из четырёх дуг эллипсов, а близкую к ней окружность^[46].

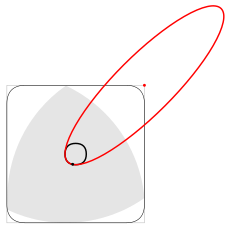Эллипс (выделен красным цветом), очерчивающий одну четвёртую кривой, по которой движется центр треугольника Рёло при вращении в квадрате	Траектория центра треугольника Рёло при вращении в квадрате. Выделены точки сопряжения четырёх дуг эллипсов. Для сравнения показана окружность (синим цветом), проходящая через эти же четыре точки

Площадь каждого из четырёх не затронутых вращением уголков равна

β=a2⋅(1−32−π24){\displaystyle \beta =a^{2}\cdot \left(1-{{\sqrt {3}} \over {2}}-{{\pi } \over {24}}\right)}^[47]

и, вычитая их из площади квадрата, можно получить площадь фигуры, которую образует треугольник Рёло при вращении в нём

a2−4β=a2⋅(23+π6−3)=a2⋅0,98770…{\displaystyle a^{2}-4\beta =a^{2}\cdot \left(2{\sqrt {3}}+{{\pi } \over {6}}-3\right)=a^{2}\cdot 0{,}98770\ldots }^[38][47][48]

Разница с площадью квадрата составляет ≈1,2 %, поэтому на основе треугольника Рёло создают свёрла, позволяющие получать почти квадратные отверстия^[45].

Сверление квадратных в сечении к оси фрезы отверстий[править | править код]

«Мы все слыхали о гаечных ключах, приспособленных для гаек с левой резьбой, завязанных в узел водопроводных трубах и бананах из чугуна. Мы считали подобные вещи смешными безделушками и отказывались даже верить, что они когда-нибудь встретятся нам в действительности. И вдруг появляется инструмент, позволяющий сверлить квадратные отверстия!»

рекламная листовка фирмы
Watts Brothers Tool Works^{[49][* 7]}

Фреза с сечением в виде треугольника Рёло и режущими лезвиями, совпадающими с его вершинами, позволяет получать почти квадратные отверстия. Отличие таких отверстий от квадрата в сечении состоит лишь в немного скруглённых углах^[50]. Другая особенность подобной фрезы заключается в том, что его ось при вращении не должна оставаться на месте, как это происходит в случае традиционных спиральных свёрл, а описывает в плоскости сечения кривую, состоящую из четырёх дуг эллипсов. Поэтому патрон, в котором зажата фреза, и крепление инструмента не должно препятствовать этому движению^[45].

Впервые реализовать подобную конструкцию крепления инструмента удалось Гарри Уаттсу, английскому инженеру, работавшему в США. Для этого он использовал направляющую пластину с отверстием в виде квадрата, в котором могло радиально перемещаться сверло, зажатое в «плавающем патроне»^[50]. Патенты на патрон^[51] и сверло^[52] были получены Уаттсом в 1917 году. Продажу новых дрелей осуществляла фирма Watts Brothers Tool Works^[en][53][54]. Ещё один патент США на похожее изобретение был выдан в 1978 году^[55].

Двигатель Ванкеля[править | править код]

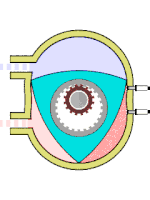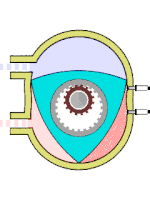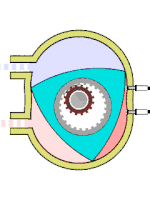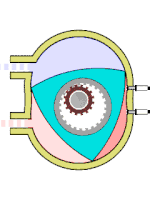Схема работы двигателя Ванкеля

Другой пример использования можно найти в двигателе Ванкеля: ротор этого двигателя выполнен в виде треугольника Рёло^[6]. Он вращается внутри камеры, поверхность которой выполнена по эпитрохоиде^[56]. Вал ротора жёстко соединён с зубчатым колесом, которое сцеплено с неподвижной шестернёй. Такой трёхгранный ротор обкатывается вокруг шестерни, всё время касаясь вершинами внутренних стенок двигателя и образуя три области переменного объёма, каждая из которых по очереди является камерой сгорания^[6]. Благодаря этому двигатель выполняет три полных рабочих цикла за один оборот.

Двигатель Ванкеля позволяет осуществить любой четырёхтактный термодинамический цикл без применения механизма газораспределения. Смесеобразование, зажигание, смазка, охлаждение и пуск в нём принципиально такие же, как у обычных поршневых двигателей внутреннего сгорания^[56].

Грейферный механизм[править | править код]

Рамочно-кулачковый грейферный механизм кинопроектора «Луч-2»

Ещё одно применение треугольника Рёло в механике — это грейферный механизм, осуществляющий покадровое перемещение плёнки в кинопроекторах. Грейфер проектора «Луч-2», например, основан на треугольнике Рёло, который вписан в рамку-квадрат и закреплён на двойном параллелограмме. Вращаясь вокруг вала привода, треугольник двигает рамку с расположенным на ней зубом. Зуб входит в перфорацию киноплёнки, протаскивает её на один кадр вниз и выходит обратно, поднимаясь затем к началу цикла. Его траектория тем ближе к квадрату, чем ближе к вершине треугольника закреплён вал (идеально квадратная траектория позволила бы проецировать кадр в течение ¾ цикла)^[6][57][58].

Существует и другая конструкция грейфера, также основанная на треугольнике Рёло. Как и в первом случае, рамка этого грейфера совершает возвратно-поступательное движение, однако её двигает не один, а два кулачка, работа которых синхронизирована с помощью зубчатой передачи^[28].

Крышки для люков[править | править код]

В форме треугольника Рёло можно изготавливать крышки для люков — благодаря постоянной ширине они не могут провалиться в люк^[59].

В Сан-Франциско, для системы рекуперирования воды^[en] корпуса люков имеют форму треугольника Рёло, но их крышки имеют форму равносторонних треугольников.

Кулачковый механизм[править | править код]

Внешние изображения
Кулачковые механизмы на основе треугольника Рёло
	Модели L01[60], L02[61] и L06[62] из коллекции механизмов Франца Рёло

Треугольник Рёло использовался в кулачковых механизмах некоторых паровых двигателей начала XIX века. В этих механизмах вращательное движение кривошипа поворачивает треугольник Рёло, прикреплённый к толкателю передаточными рычагами, что заставляет толкатель совершать возвратно-поступательное движение^[63]. По терминологии Рёло, это соединение образует «высшую» кинематическую пару, поскольку контакт звеньев происходит по линии, а не по поверхности^[64]. В подобных кулачковых механизмах толкатель при достижении крайнего правого или левого положения остаётся некоторое конечное время неподвижен^[63][10].

Треугольник Рёло ранее широко применялся в кулачковых механизмах швейных машин зигзагообразной строчки.

В качестве кулачка треугольник Рёло использовали немецкие часовые мастера в механизме наручных часов A. Lange & Söhne «Lange 31»^[65].

Каток[править | править код]

Для перемещения тяжёлых предметов на небольшие расстояния можно использовать не только колёсные, но и более простые конструкции, например, цилиндрические катки^[66]. Для этого груз нужно расположить на плоской подставке, установленной на катках, а затем толкать его. По мере освобождения задних катков их необходимо переносить и класть спереди^[67][66]. Такой способ транспортировки человечество использовало до изобретения колеса.

При этом перемещении важно, чтобы груз не двигался вверх и вниз, так как тряска потребует дополнительных усилий от толкающего^[67]. Для того, чтобы движение по каткам было прямолинейным, их сечение должно представлять собой фигуру постоянной ширины^[67][68]. Чаще всего сечением был круг, ведь катками служили обыкновенные брёвна. Однако сечение в виде треугольника Рёло будет ничуть не хуже

Ответы Mail.ru: Треугольный квадрат — это как ?))

Это как конечный круг! Ну или квадратура круга)))

ну, как квадратный круг

Это прямоугольный круг

ты должен сламать сепе моск

Такого не бывает.

<img src=»//otvet.imgsmail.ru/download/u_08e46223ad5af6cfedded281c48288da_800.jpg» alt=»» data-lsrc=»//otvet.imgsmail.ru/download/u_08e46223ad5af6cfedded281c48288da_120x120.jpg» data-big=»1″>

Это прикольно если трава хорошая

I need drugs. <img src=»//otvet.imgsmail.ru/download/205353696_26c5c69b1e9d50d0e3d4bfeccf6ce24f_800.jpg» data-lsrc=»//otvet.imgsmail.ru/download/205353696_26c5c69b1e9d50d0e3d4bfeccf6ce24f_120x120.jpg»>

это жёстко тебя накрыло

Это тест для пациентов Кащенко…

Берем к примеру землю, допустим, что она — идеальный шар. Если мы начнем на экваторе некий путь, пойдем на один из полюсов, повернем на 90 градусов и снова остановимся на экваторе, снова повернем на 90 градусов и вернемся к нашей начальной точки. Вырежем фигуру по контурам нашего пути (можно взять глобус) и получается треугольный квадрат. Подробнее в источнике

Треугольный квадрат существует только на сфере, если учесть условие что у квадрата все стороны равны и углы раны 90 градусам, а вот на «псевдо сфере» можно получить пятиугольный квадрат.